Discovery of Quasi-crystals

10/10/1982View on timeline

Daniel Shechtman, Israeli chemist who was awarded the 2011 Nobel Prize for Chemistry for his discovery of quasicrystals, a type of crystal in which the atoms are arranged in a pattern that follows mathematical rules but without the pattern ever repeating itself.

In 1982, while on sabbatical at the National Bureau of Standards (now the National Institute of Standards and Technology) in Gaithersburg, Maryland, Shechtman was investigating the metallurgical properties of aluminum-iron and aluminum-manganese alloys for a research program sponsored by the Defense Advanced Research Projects Agency. Shechtman and his colleagues mixed aluminum and manganese in a roughly six-to-one proportion; they then heated the mixture and, once it melted, rapidly cooled it back into the solid state. Using an electron microscope, Shechtman found that the solidified alloy unexpectedly displayed fivefold symmetry; that is, rotating it by 72° (360°/5) reproduced the same structure. Such a symmetry was considered impossible in crystals, since it could not provide the basis of a repeating, regular structure. The alloy’s structure was aperiodic (i.e., it did not repeat).

Shechtman was vilified for insisting that he had discovered a crystal with a fivefold symmetry and an aperiodic structure; the types of structures possible in a crystal had been considered a closed subject since the 1890s. Shechtman was asked to leave his research group at the National Bureau of Standards, and it was not until 1984 that he was able to publish his findings. Later that year American physicist Paul Steinhardt and Israeli physicist Dov Levine coined the term quasicrystal to describe Shechtman’s discovery. Even then, few scientists were convinced. American chemist Linus Pauling was particularly vehement, saying, “There are no quasicrystals, only quasi-scientists.” Many crystallographers, who used X-rays in their work, were reluctant to accept Shechtman’s findings, which were produced with an electron microscope. In 1987 Shechtman was vindicated when scientists in France and Japan made quasicrystals that were large enough to be examined with X-rays.

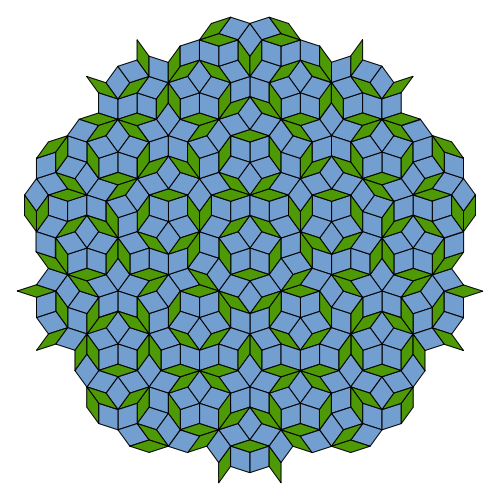
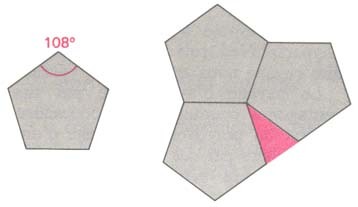
A quasiperiodic crystal, or quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry. While crystals, according to the classical crystallographic restriction theorem, can possess only two, three, four, and six-fold rotational symmetries, the Bragg diffraction pattern of quasicrystals shows sharp peaks with other symmetry orders, for instance five-fold.

Aperiodic tilings were discovered by mathematicians in the early 1960s, and, some twenty years later, they were found to apply to the study of quasicrystals. The discovery of these aperiodic forms in nature has produced a paradigm shift in the fields of crystallography. Quasicrystals had been investigated and observed earlier, but, until the 1980s, they were disregarded in favor of the prevailing views about the atomic structure of matter. In 2009, after a dedicated search, a mineralogical finding, icosahedrite, offered evidence for the existence of natural quasicrystals.

Roughly, an ordering is non-periodic if it lacks translational symmetry, which means that a shifted copy will never match exactly with its original. The more precise mathematical definition is that there is never translational symmetry in more than n – 1 linearly independent directions, where n is the dimension of the space filled, e.g., the three-dimensional tiling displayed in a quasicrystal may have translational symmetry in two directions. Symmetrical diffraction patterns result from the existence of an indefinitely large number of elements with a regular spacing, a property loosely described as long-range order. Experimentally, the aperiodicity is revealed in the unusual symmetry of the diffraction pattern, that is, symmetry of orders other than two, three, four, or six. In 1982 materials scientist Dan Shechtman observed that certain aluminium-manganese alloys produced the unusual diffractograms which today are seen as revelatory of quasicrystal structures. Shechtman first observed ten-fold electron diffraction patterns in 1982, as described in his notebook. The observation was made during a routine investigation, by electron microscopy, of a rapidly cooled alloy of aluminium and manganese prepared at the US National Bureau of Standards (later NIST).

Potential energy surface for silver depositing on an aluminium-palladium-manganese (Al-Pd-Mn) quasic...

The observation of the ten-fold diffraction pattern lay unexplained for two years until the spring of 1984, when Blech asked Shechtman to show him his results again. A quick study of Shechtman's results showed that the common explanation for a ten-fold symmetrical diffraction pattern, the existence of twins, was ruled out by his experiments. Since periodicity and twins were ruled out, Blech, unaware of the two-dimensional tiling work, was looking for another possibility: a completely new structure containing cells connected to each other by defined angles and distances but without translational periodicity. Blech decided to use a computer simulation to calculate the diffraction intensity from a cluster of such a material without long-range translational order but still not random. He termed this new structure multiple polyhedral.

The idea of a new structure was the necessary paradigm shift to break the impasse. The “Eureka moment” came when the computer simulation showed sharp ten-fold diffraction patterns, similar to the observed ones, emanating from the three-dimensional structure devoid of periodicity. The multiple polyhedral structure was termed later by many researchers as icosahedral glass but in effect it embraces any arrangement of polyhedra connected with definite angles and distances (this general definition includes tiling, for example).

Ten-fold way. Quasiperiodic patterns have small repeating elements but on a larger scale do not exac...

It took two years before the paper was published, as Schechtman and his colleagues did careful checks to rule out other possibilities, for example, that the unexpected spots could have come from crystalline regions with different orientations. In the end, they showed that the icosahedral symmetry extended over distances of microns, thousands of times larger than the atomic spacing.

Within six weeks after the publication, Dov Levine and Paul Steinhardt, then at the University of Pennsylvania in Philadelphia, published another paper in Physical Review Letters that resolved the mystery of a crystal with five-fold symmetry and introduced the term “quasicrystal”. The icosahedral symmetry was permitted, they said, as long as the structure was only “quasi-periodic.” For example, if a pattern contains two elements that repeat with different periods, and the ratio of those periods is irrational, they will never “synchronize,” even over very long distances. Because they do not quite repeat, such patterns can evade the usual prohibitions on certain rotational symmetries.

Roger Penrose of Oxford University in England had toyed with such patterns in the 1970s, and the same mathematical rules appear in Islamic architecture from centuries earlier. But no one expected to see them appear in a real material, especially since they seemed to require painstaking construction of the whole, infinite pattern all at once. Subsequent researchers showed that quasiperiodic structures could be assembled atom-by-atom by following only the sort of local rules that must govern the growth of real crystals.

Materials Science

Since the original discovery by Dan Shechtman, hundreds of quasicrystals have been reported and confirmed. Undoubtedly, the quasicrystals are no longer a unique form of solid; they exist universally in many metallic alloys and some polymers. Quasicrystals are found most often in aluminium alloys (Al-Li-Cu, Al-Mn-Si, Al-Ni-Co, Al-Pd-Mn, Al-Cu-Fe, Al-Cu-V, etc.), but numerous other compositions are also known (Cd-Yb, Ti-Zr-Ni, Zn-Mg-Ho, Zn-Mg-Sc, In-Ag-Yb, Pd-U-Si, etc.).

Two types of quasicrystals are known. The first type, polygonal (dihedral) quasicrystals, have an axis of 8, 10, or 12-fold local symmetry (octagonal, decagonal, or dodecagonal quasicrystals, respectively). They are periodic along this axis and quasiperiodic in planes normal to it. The second type, icosahedral quasicrystals, are aperiodic in all directions.

Quasicrystals fall into three groups of different thermal stability:

Stable quasicrystals grown by slow cooling or casting with subsequent annealing,
Metastable quasicrystals prepared by melt spinning, and
Metastable quasicrystals formed by the crystallization of the amorphous phase.

Except for the Al–Li–Cu system, all the stable quasicrystals are almost free of defects and disorder, as evidenced by X-ray and electron diffraction revealing peak widths as sharp as those of perfect crystals such as Si. Diffraction patterns exhibit fivefold, threefold, and twofold symmetries, and reflections are arranged quasiperiodically in three dimensions.

The origin of the stabilization mechanism is different for the stable and metastable quasicrystals. Nevertheless, there is a common feature observed in most quasicrystal-forming liquid alloys or their undercooled liquids: a local icosahedral order. The icosahedral order is in equilibrium in the liquid state for the stable quasicrystals, whereas the icosahedral order prevails in the undercooled liquid state for the metastable quasicrystals.

A nanoscale icosahedral phase was formed in Zr-, Cu- and Hf-based bulk metallic glasses alloyed with noble metals.

Most quasicrystals have ceramic-like properties including high thermal and electrical resistance, hardness and brittleness, resistance to corrosion, and non-stick properties.[39] Many metallic quasicrystalline substances are impractical for most applications due to their thermal instability; the Al-Cu-Fe ternary system and the Al-Cu-Fe-Cr and Al-Co-Fe-Cr quaternary systems, thermally stable up to 700 °C, are notable exceptions.

Tiling of a plane by regular pentagons is impossible but can be realized on a sphere in the form of...

A Ho-Mg-Zn icosahedral quasicrystal formed as a pentagonal dodecahedron, the dual of the icosahedron...

Applications

Quasicrystalline substances have potential applications in several forms.

Metallic quasicrystalline coatings can be applied by plasma-coating or magnetron sputtering. A problem that must be resolved is the tendency for cracking due to the materials' extreme brittleness. The cracking could be suppressed by reducing sample dimensions or coating thickness. Recent studies show typically brittle quasicrystals can exhibit remarkable ductility of over 50% strains at room temperature and sub-micrometer scales (<500 nm).

An application was the use of low-friction Al-Cu-Fe-Cr quasicrystals as a coating for frying pans. Food did not stick to it as much as to stainless steel making the pan moderately non-stick and easy to clean; heat transfer and durability were better than PTFE non-stick cookware and the pan was free from perfluorooctanoic acid (PFOA); the surface was very hard, claimed to be ten times harder than stainless steel, and not harmed by metal utensils or cleaning in a dishwasher; and the pan could withstand temperatures of 1,000 °C (1,800 °F) without harm. However, cooking with a lot of salt would etch the quasicrystalline coating used, and the pans were eventually withdrawn from production. Shechtman had one of these pans.

The Nobel citation said that quasicrystals, while brittle, could reinforce steel "like armor". When Shechtman was asked about potential applications of quasicrystals he said that a precipitation-hardened stainless steel is produced that is strengthened by small quasicrystalline particles. It does not corrode and is extremely strong, suitable for razor blades and surgery instruments. The small quasicrystalline particles impede the motion of dislocation in the material.

Quasicrystals were also being used to develop heat insulation, LEDs, diesel engines, and new materials that convert heat to electricity. Shechtman suggested new applications taking advantage of the low coefficient of friction and the hardness of some quasicrystalline materials, for example embedding particles in plastic to make strong, hard-wearing, low-friction plastic gears. The low heat conductivity of some quasicrystals makes them good for heat insulating coatings.

Other potential applications include selective solar absorbers for power conversion, broad-wavelength reflectors, and bone repair and prostheses applications where biocompatibility, low friction and corrosion resistance are required. Magnetron sputtering can be readily applied to other stable quasicrystalline alloys such as Al-Pd-Mn.

While saying that the discovery of icosahedrite, the first quasicrystal found in nature, was important, Shechtman saw no practical applications.